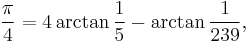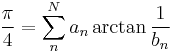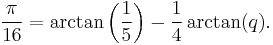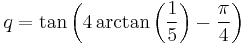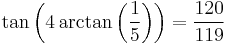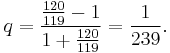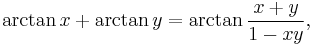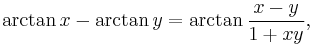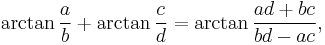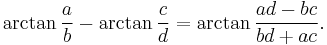Machin-like formula
In mathematics, Machin-like formulae are a class of identities involving π = 3.14159... that generalize John Machin's formula from 1706:
which he used along with the Taylor series arctangent expansion to compute π to 100 decimal places.
Machin-like formulas have the form
with 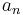 and
and 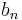 integers.
integers.
The same method is still among the most efficient known for computing a large number of digits of π with digital computers.
Contents |
Derivation
To understand where this formula comes from, start with following basic ideas:
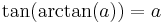
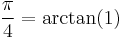
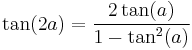 (tangent double angle identity)
(tangent double angle identity)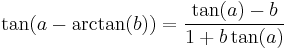 (tangent difference identity)
(tangent difference identity)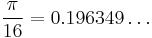 (approximately)
(approximately)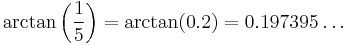 (approximately)
(approximately)
In other words, for small numbers, arctangent is to a good approximation just the identity function. This leads to the possibility that a number  can be found such that
can be found such that
Using elementary algebra, we can isolate  :
:
Using the identities above, we substitute arctan(1) for π/4 and then expand the result.
Similarly, two applications of the double angle identity yields
and so
Other formulas may be generated using complex numbers. For example the angle of a complex number a+bi is given by 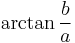 and when you multiply complex numbers you add their angles. If a=b then
and when you multiply complex numbers you add their angles. If a=b then 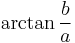 is 45 degrees or
is 45 degrees or 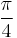 . This means that if the real part and complex part are equal then the arctangent will equal
. This means that if the real part and complex part are equal then the arctangent will equal 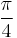 . Since the arctangent of one has a very slow convergence rate if we find two complex numbers that when multiplied will result in the same real and imaginary part we will have a Machin-like formula. An example is
. Since the arctangent of one has a very slow convergence rate if we find two complex numbers that when multiplied will result in the same real and imaginary part we will have a Machin-like formula. An example is 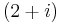 and
and 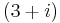 . If we multiply these out we will get
. If we multiply these out we will get 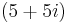 . Therefore
. Therefore 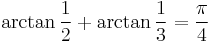 .
.
If you want to use complex numbers to show that 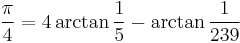 you first must know that when multiplying angles you put the complex number to the power of the number that you are multiplying by. So
you first must know that when multiplying angles you put the complex number to the power of the number that you are multiplying by. So 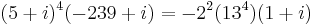 and since the real part and imaginary part are equal then,
and since the real part and imaginary part are equal then, 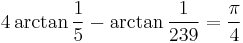
Two-term formulas
There are exactly three additional Machin-like formulas with two terms; these are Euler's
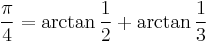 ,
,
Hermann's,
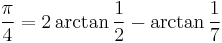 ,
,
and Hutton's
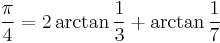 .
.
More terms
The 2002 record for digits of π, 1,241,100,000,000, was obtained by Yasumasa Kanada of Tokyo University. A 64-node Hitachi supercomputer with 1 terabyte of main memory, performing 2 trillion operations per second, was used to evaluate the following Machin-like formulas:
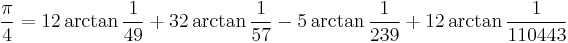
- Kikuo Takano (1982).
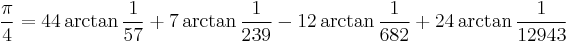
- F. C. W. Störmer (1896).
The more efficient currently known Machin-like formulas for computing:
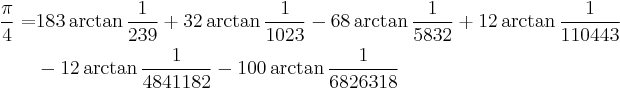
- 黃見利(Hwang Chien-Lih) (1997).

- 黃見利(Hwang Chien-Lih) (2003).
These Machin-like formula is shown by the following identities;
or equivalently,
These identities are easily derived from the definition of arctangent. With these identities, we shall show the Machin-like formula such as Takano;
 :
:
External links
- Weisstein, Eric W., "Machin-like formulas" from MathWorld.
- The constant π
- Machin's Merit at MathPages
- Archimedes' constant pi - Machin's formula gives a proof for the John Machin`s formula